Plano de estudos de Matemática: estude para Enem e vestibulares

Você já deve saber que dominar os temas da Matemática é fundamental para garantir uma boa nota no Enem e nos vestibulares, não é? Além disso, várias opções de formação exigem que o aluno tenha um bom desempenho nessa área.

Pensando nisso, vamos te ajudar a montar um plano de estudos com o essencial de Matemática para as provas de ingresso ao ensino superior. Neste material, apresentamos os temas mais recorrentes e fundamentais da Matemática. Não deixe, ao fim da leitura, de treinar seus conhecimentos.

Vamos conhecer os principais assuntos? Vem com a gente!

Quais matérias de Matemática caem no Enem e vestibulares?

O caderno de Matemática e suas tecnologias no Exame Nacional do Ensino Médio (Enem) conta com 45 questões, e possui uma variedade de tópicos frequentes, desde questões mais simples até as mais complexas, que exigem do aluno concentração e domínio.

Antes de indicarmos quais os conteúdos mais frequentes, vale a pena conhecer o guia completo do Enem, para entender a estrutura da prova, além de receber dicas para otimizar o seu tempo e aumentar as chances de tirar uma boa nota.

O Enem é a principal forma de ingresso ao ensino superior, mas não é a única. Muitos alunos podem realizar provas de vestibular para ingressar em instituições de todo o Brasil, que contam com um número limitado de vagas, por isso, executam formas de seleção para preenchê-las.

Acompanhe, agora, os assuntos mais frequentes nas provas de Matemática do Enem e vestibulares:

Leitura de gráficos e tabelas

A boa interpretação dos recursos visuais como gráficos e tabelas é uma das exigências mais comuns para que o aluno se saia bem nas provas. Essas ferramentas reúnem informações e dados, e são resumos mais atrativos para a leitura de estudos, cálculos e estatísticas.

Os gráficos apresentam informações quantitativas ou qualitativas, traduzindo conceitos matemáticos. Os dados são organizados por pontos, linhas e formas geométricas, que criam relações entre si. Cada fenômeno possui diversas dimensões, padrões ou tendências, e as informações disponíveis em bases de dados podem ser comparadas ou determinadas de acordo com o tema de interesse.

Em questões do Enem e vestibular, é muito comum que os alunos tenham que interpretar ou inferir informações que tenham como base os gráficos. Eles possuem alguns elementos dos quais vale a pena se atentar.

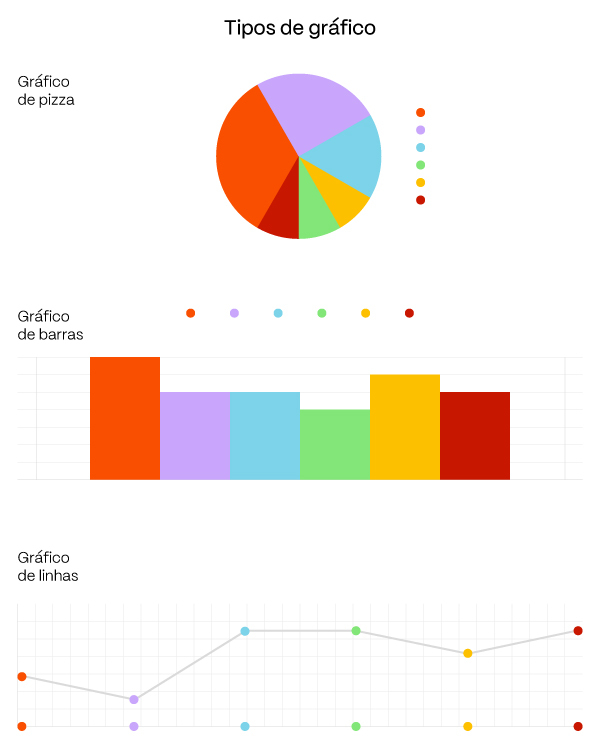
Todo gráfico possui um título com palavras-chave sobre o assunto apresentado, que deve ser acompanhado de uma fonte dos dados, geralmente presente na parte inferior. Os gráficos são compostos também por números em ordem crescente, que são essenciais para o estabelecimento de análises e comparações.

Nos cantos do gráfico é comum observar unidades de medidas, que servem para guiar a interpretação das informações. Exemplos são quilômetro (km) e hora (h), assim, um gráfico pode traçar em seus eixos como um carro progride na aceleração, e com isso mostrar a relação entre os quilômetros percorridos a cada hora de uma determinada movimentação.

As legendas auxiliam a resumir as informações a serem analisadas num gráfico, e devem estar destacadas. Elas podem estar presentes em qualquer parte do gráfico, e são uma ferramenta essencial para entender os números e as formas ilustrativas.

Os tipos mais comuns de gráfico são os de colunas ou barras, utilizados em comparações, os de linhas ou segmentos, que indicam evolução, regressão e tendências, e os de pizza ou setores, adequados para a representação de estatísticas, porcentagens, e divisão em partes que resultam no todo de 100%.

As informações de base para a produção de um gráfico geralmente estão contidas em uma tabela, por isso, é muito comum observá-las lado a lado. Enquanto a interpretação de uma tabela pode não sugerir efeitos como o de causa e consequência, o gráfico consegue guiar análises pela sua natureza de imagem.

 As tabelas são organizadas com linhas e colunas, além de também possuírem títulos e fontes dos dados. As informações dispostas nas linhas podem indicar variáveis, tendências, ou mesmo a estabilidade numérica do que é exposto.

Por exemplo, de acordo com a tabela acima, poderia ser elaborado um gráfico resumindo as informações e promovendo uma lógica de análise. Mas a tabela, por si só, já funciona como um item com conclusões possíveis e interpretações lógicas de acordo com o comando das questões.

Agora que você já entendeu como proceder com gráficos e tabelas nas provas do Enem e vestibulares, vamos conhecer um pouco mais sobre os outros assuntos.

Escalas, razões e proporções

As escalas, razões e proporções se relacionam pelo tipo de operação matemática que envolve todos esses assuntos: a divisão. É comum chamarmos em matemática, divisões de razões. Uma razão representa a razão entre dois números.

As escalas matemáticas são razões entre medidas de uma figura ou representação e a realidade. Isso quer dizer que cada vez que aparece um mapa ou uma planta para a análise, as distâncias indicadas são proporcionais ao tamanho dos objetos na realidade.

As legendas dispostas nos mapas são um exemplo da indicação de proporcionalidade. Se um mapa diz que 1cm:100 km, deve-se compreender que cada 1cm de território do mapa corresponde a 100 km na realidade. Ou seja, as medidas presentes podem ser utilizadas para estimar tamanhos e distâncias.

Estudos em Geografia ou Engenharia usam constantemente as escalas, seja para construir mapas ou para planejar obras. É importante observar que os valores reduzidos são formas de dispor as informações da realidade que não poderiam ser expressos numa folha de papel.

A razão, que já discutimos acima, pode ser expressa de diferentes maneiras. Considere a e b como números inteiros:

1. a:b;
2. a/b;
3. a está para b.

Chamamos “a” de termo antecedente ou numerador da divisão, e “b” termo consequente ou denominador da divisão. Deve-se atentar para algumas razões específicas, que são lidas de maneira diferente, como nas frações, em que ⅔ se lê dois terços, e não “dois está para três”.

As proporções são duas ou mais razões que possuem o mesmo resultado, como por exemplo:

• ¾ = 6/8.
• 3:4 = 6:8.

Nesse caso, os resultados da divisão são idênticos, e os valores proporcionais. Essas noções ajudam a explicar desde tarefas simples, como a preparação de receitas, até a seleção de materiais para uma construção industrial.

Além disso, razão e proporção são a base das regras de três, que consideram que dois termos relacionados proporcionais e possuem uma incógnita x. As regras de três ajudam a descobrir valores ocultos ou omitidos, além de permitir a realização de inferências.

Estatística e probabilidade

“As estatísticas não mentem” é um divertido ditado que ilustra como muitos dos dados utilizados no cotidiano, por governos ou mesmo para a realização de exames é baseado na estatística. Juntas, estatística e probabilidade estão relacionadas ao ramo da Matemática.

Esse ramo da ciência se relaciona com a coleta, organização, análise e apresentação de dados de certa forma concretos. Ela se baseia na organização de informações numéricas e também na compreensão de fenômenos a partir de técnicas utilizadas em larga escala.

Os estudos estatísticos têm origem no século XVII, com o inglês John Graunt como um dos principais nomes relacionados ao uso dos métodos. Nos estudos desse pesquisador, foram publicados dados sobre número de mortes e nascimentos em Londres.

Hoje em dia, a estatística se desenvolveu e pode ser estudada em diferentes áreas:

• Estatística descritiva: trata-se de uma metodologia de apresentação de dados com alta confiabilidade, um exemplo é o censo populacional do Instituto Brasileiro de Geografia Estatística (IBGE).
• Estatística inferencial: trata da coleta de dados de uma amostra de um todo para analisar o todo, tendo como exemplo as pesquisas eleitorais ou os exames de sangue.

Alguns conceitos da estatística são a chave para entender muitos estudos. População, por exemplo, é um conjunto de elementos ou pessoas com pelo menos uma característica em comum, utilizada como informação para considerar se esse dado pertence ou não a população. Já a amostra, mencionada acima, é um subconjunto representativo da população.

Além disso, as pesquisas trabalham com variáveis qualitativas e quantitativas, que são características dos indivíduos da amostra que são relevantes para uma análise. Por fim, os resultados estatísticos são posicionados entre tendências centrais, dispersão ou variabilidade, para entender que conclusões podem ser realizadas a partir de um conjunto de dados.

Já a probabilidade, um assunto próximo a estatística, tem mais a ver com as chances de um evento ou fenômeno acontecer. Essas chances são, por definição, expressas numa porcentagem de 0 a 100%, ou num número entre 0 e 1.

Algumas questões comuns em probabilidade permeiam o cotidiano, como chances de ser atingido por um raio, vencer na loteria ou mesmo acertar qual das faces de uma moeda estará virada para cima ao cair no chão. Essa área de estudos analisa fenômenos aleatórios.

Para facilitar os cálculos, podemos aplicar a fórmula da probabilidade:

Onde:

P(A): chance de um evento A ocorrer;

n(A): número de casos de interesse ou favoráveis ao evento A;

n(Ω): número de casos possíveis.

A probabilidade se consolidou como uma ciência a partir de jogos de dados entre matemáticos, que observaram, por exemplo, as chances de uma das faces de um dado ser o resultado do jogo dentre todas as 6 possibilidades.

Alguns termos ajudam a entender os conceitos, como eventos aleatórios, que são a base para as indagações em probabilidade. Já os pontos amostrais são resultados possíveis desses experimentos, e compõem o número de casos possíveis.

Os eventos, por sua vez, são subconjuntos dos espaços amostrais, desde o número 0 (um evento impossível) até os eventos certos (todos os resultados possíveis). No exemplo que usamos acima, dos dados, não é possível que o resultado de um jogo seja um número menor que 1 ou maior que 6, sendo assim, a probabilidade disso ocorrer é nula.

Cotidianamente, as pessoas calculam possibilidades analisando as situações e o universo de possibilidades, fazendo com que esse conceito seja usual e bastante próximo a realidade dos alunos.

Geometria

A área da geometria se dedica aos estudos sobre as formas dos objetos, suas posições, dimensões, tendo em vista que os objetos podem ser figuras planas ou espaciais. Esses estudos também vão além, considerando o espaço ocupado pelos objetos e as dimensões dos planos de imagem.

Esses estudos surgiram na Grécia Antiga e no Egito, há muitos séculos atrás, com a construção de monumentos. Para que essas construções ocorressem e dessem certo, as populações da época precisavam de um sistema de medidas bem estruturado.

O estudioso considerado o pai da geometria é o matemático grego Euclides. Outros pensadores, teóricos e filósofos da Idade Antiga desenvolveram estudos, teoremas, leis e demais aplicações presentes na matemática até os dias de hoje. São eles: Reneé Descartes, Tales de Mileto, Apolônio, Arquimedes, Pitágoras, dentre outros.

A geometria se divide em áreas de estudo:

1. A geometria plana ou Euclidiana busca compreender espaço e plano, de acordo com os pontos do postulado de Euclides. Essa área estuda objetos que não possuem volume, sendo assim, foca no perímetro, lado ou forma de uma figura matemática.
2. Já a geometria espacial reúne as formas matemáticas considerando que elas ocupam espaço, ou seja, possuem dimensões como altura, largura e comprimento, logo, pode-se afirmar que esse é o estudo das figuras que possuem volume, como os cubos, cilindros e pirâmides.
3. A geometria analítica representa questões e análises algébricas, e se baseia no plano cartesiano, incluindo nos estudos os conceitos de ponto e reta, além das coordenadas gráficas. Os estudos analíticos dessa área da geometria são compartilhados com outras ciências, como a física.

As figuras geométricas aparecem nas provas em questões e problemas que possuem fórmulas específicas para os cálculos geralmente relacionados com área, volume, etc.

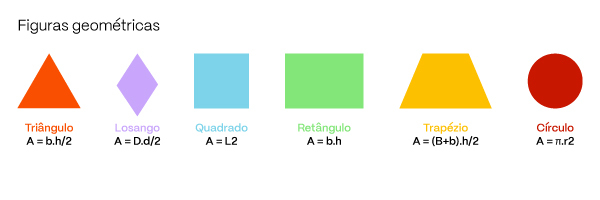
• Quadrado (figura): A = L2.
• Triângulo (figura): A = b.h/2.
• Retângulo (figura): A = b.h.
• Losango (figura): A = D.d/2.
• Trapézio (figura): A = (B+b).h/2.
• Círculo (figura): A = π.r2.

No caso de um círculo, cabe lembrar que o comprimento da circunferência (C) vale C = 2.π.r, e que nesses estudos o valor de π = 180º.

Alguns cursos se conectam mais com o estudo de formas geométricas. Vamos citar alguns exemplos: Arquitetura e Urbanismo, Engenharia, Agrimensura, Matemática, Astronomia, Design Gráfico, Ciência da Computação, dentre outros.

Trigonometria e funções

A trigonometria estuda as relações em um triângulo, entre os lados e os ângulos formados, e constitui conhecimentos para aplicações em diversas áreas do conhecimento.

A história da trigonometria é incerta, tendo o Papiro Rhind e a tábua cuneiforme Plimpton 322 como os prováveis primeiros documentos históricos a tratarem desse  conhecimento. Em 1855, o advogado escocês A. H. Rhind identificou no Papiro Rhind textos matemáticos compatíveis com a trigonometria.

Estudiosos gregos, como Euclides de Alexandria, contribuíram para o desenvolvimento da trigonometria com formas geométricas, lei dos cossenos, estudo dos ângulos. Mas Hiparco de Niceia é o estudioso considerado o “pai da trigonometria”, que no século II a.C produziu e apresentou um tratado que aprofundou os conhecimentos em trigonometria.

Ptolomeu, um contemporâneo desses estudiosos, apresentou uma tábua de cordas em que calculava o senho dos ângulos de 0 a 90º, além de produzir a Syntaxis Mathematica, uma das obras mais importantes da história.

A trigonometria estuda, principalmente, o triângulo retângulo. Esse tipo de polígono possui um ângulo reto (90º) e ângulos menores, conhecidos como agudos. A soma dos ângulos retos e agudos deve sempre ser de 180º.

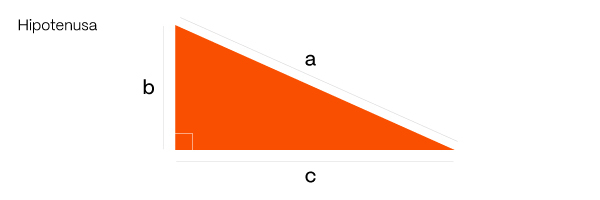
O maior lado do triângulo, oposto ao ângulo reto, é chamado de hipotenusa, enquanto os catetos são os outros dois. O cateto adjacente está sempre ao mesmo lado do ângulo de referência do triângulo, e o oposto ao contrário.

Foi com essas considerações que se observou o desenvolvimento do Teorema de Pitágoras, que enuncia: a hipotenusa ao quadrado é igual a soma dos quadrados dos catetos.

Sendo assim, esse enunciado se traduz na fórmula:

a² = b² + c², em que “a” é a hipotenusa, e “b” e “c” são os catetos.

Outro foco da trigonometria são os círculos trigonométricos, ciclos ou circunferências. São formas circulares com raio 1 e centro localizado no ponto (0,0) de um plano cartesiano. Ele é cortado por duas retas perpendiculares entre si, e dividido em quadrantes.

Dentro de um círculo, diferente dos triângulos, as medidas são identificadas em graus ou radianos. A proporção é a seguinte:

• 2pi radianos (rad) = 360º.
• pi radianos (rad) = 180º.
• pi/2 radianos (rad) = 90º
• pi/3 radianos (rad) = 60º.
• pi/4 radianos (rad) = 45º.

Os quadrantes, que apresentamos acima, são dispostos no sentido anti-horário e correspondem aos seguintes ângulos:

• 1º quadrante: 0 a 90º;
• 2º quadrante: 90 a 180º;
• 3º quadrante: 180 a 270º;
• 4º quadrante: 270 a 360º.

Dentro desse assunto, se entende que num triângulo existem razões trigonométricas, o seno, o cosseno e a tangente. Essas razões são resultados de divisões entre dois lados de um triângulo retângulo.

Essas razões podem ser consideradas funções periódicas, com valores que se repetem em intervalos ou períodos. Por isso, é muito comum que se considere valores fixos para ângulos específicos dentro de triângulos ou dos círculos trigonométricos.

O seno representa a relação entre o cateto oposto e a hipotenusa do triângulo, com a fórmula:

Seno = cateto oposto/hipotenusa

Nesse caso, a função é descrita por f(x) = senx. Vale ressaltar que o seno de um ângulo é sempre positivo nos 1º e 2º quadrantes, e negativo no 3º e 4º quadrantes.

Para o caso do cosseno, a fórmula relaciona o cateto adjacente e a hipotenusa, dessa maneira:

Cosseno =cateto adjacente/hipotenusa

Definida por f(x) = cosx, a função cosseno representa os cossenos de ângulos que serão sempre positivos no 1º e 4º quadrantes e negativos no 2º e 3º quadrantes.

A tangente dos ângulos é representada por uma razão entre os catetos, nesse caso, o oposto e o adjacente de um triângulo retângulo. Sendo assim, pode ser estudada pela fórmula:

Tangente = cateto oposto/cateto adjacente

Assim como nos casos anteriores, a função tangente se define por f(x) = tgx.

Uma das considerações mais comuns em trigonometria é a dos ângulos notáveis. São os ângulos mais frequentes nos cálculos e com resultados já conhecidos. Vale a pena estudar essa tabela para compreender os resultados observados.

Esses valores devem ser considerados em diferentes tipos de questão, e podem ser fornecidos ou não. O importante é compreender que os ângulos de 30, 45 e 60º são de especial interesse para a matemática e para as áreas relacionadas.

As relações apresentadas são fundamentais e básicas, mas a trigonometria não se limita apenas aos triângulos, e é aplicada na eletricidade, mecânica, música, topologia, engenharia civil, acústica, dentre outras áreas, por isso é essencial estudar a base desse conhecimento.

Já te apresentamos as principais temáticas de matemática para o Enem e vestibulares, mas você deve estar se perguntando como se preparar para as provas. Fique tranquilo, nós pensamos nisso!

Como treinar os conhecimentos em Matemática?

Agora que você já tem um plano de estudos, busque os assuntos abordados para se aprofundar em cada um. Assim, você vai chegar no dia da prova preparado para as questões sobre esses assuntos.

Agora que você já pode montar um plano de estudos, busque os assuntos abordados nesse artigo e se aprofunde em cada um, com exemplos e exercícios de fixação. Assim, você vai chegar no dia da prova mais tranquilo e preparado para lidar com as questões sobre esses assuntos. Queremos que você tire um notão!

Aproveite para realizar nosso simulado do Enem em Matemática e suas tecnologias  e testar seus conhecimentos. Até a próxima!